Questi 3 gruppi di simmetria sono noti anche con nomi diversi e, nel campo dell'arte in particolare, sono noti con i nomi:
1) GRUPPO DEI ROSONI, perché costituiscono quelle figure caratteristiche delle chiese che si trovano o sulla facciata principale, al centro sopra la porta di ingresso, oppure si trovano nell'abside, che è la parte opposta alla facciata della chiesa e che in genere all'interno contengono l'altare dove il sacerdote celebra la messa, oppure contiene il presbiterio, cioè le sedute riservate ai religiosi; talvolta contengono entrambi qualora la lunghezza dell'abside lo consenta. I rosoni possono trovarsi anche lungo le facciate laterali della chiesa. Questo gruppo è chiamato anche Simmetria Centrale.
2) GRUPPO DEI FREGI, perché si svolgono su una superficie di una certa lunghezza ma di altezza assai limitata rispetto alla lunghezza. Vengono impiegati a scopo decorativo sia per edifici religiosi che civili, e sia all'interno che all'esterno dell'edificio stesso.
3) GRUPPO DEI MOSAICI (oppure GRUPPO CARTA DA PARATI), Il primo nome (Gruppo dei mosaici) si riferisce alla piastrellatura di pavimenti di stanze o per il rivestimento dei muri di particolari stanze come i bagni o le cucine: in questo caso sono fatte di piastrelle regolari di ceramica di forma quadrata, rettangolare, esagonale, ecc..Il secondo nome (Gruppo carta da parati) si riferisce al fatto che ricoprono tutta una superficie intera, come la carta da parati (cioè quella carta che si acquista in rotoli e che, srotolandola, viene incollata sui muri interni delle stanze di un edificio a scopo decorativo).
Il Gruppo dei rosoni è costituito da due sottogruppi: il Sottogruppo ciclico e il Sottogruppo diedrale; entrambi questi due sottogruppi sono costituiti da un numero infinito di casi, a seconda in quante parti intere dividiamo l'angolo giro che, come noto, è di 360°. Cioè possiamo dividere l'angolo giro, ad esempio. in 3 parti, ognuna delle quali è di 120° di ampiezza (= 360° / 3), oppure in 4 parti, ognuna delle quali è di 90° di ampiezza e così via, Ma non possiamo dividere l'angolo giro in 4,5 parti, ad esempio. perché avremmo 5 porzioni, una delle quali non è uguale alle altre 4 (infatti avremmo 4 porzioni di 80° ciascuna (80° x 4 = 320°) e una porzione di 40 ° (320° + 40° = 360°).
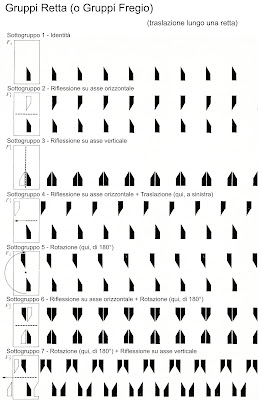
Il Gruppo dei fregi è costituito da 7 sottogruppi, e ciascun sottogruppo è costituito da un solo caso: i loro nomi possono differire a seconda dell'autore che li descrive; possono essere identificati anche da una sigla.
Il Gruppo carta da parati è costituito da 17 sottogruppi e, anche in questo caso, ciascun sottogruppo è costituito da un solo caso; i loro nomi variano anche per essi a seconda dell'autore che li descrive e possono essere identificati anche con una sigla.
Se si volesse prendere uno spazio a 3 dimensioni (cioè lo spazio ordinario che tutti conosciamo) allora il numero dei sottogruppi sarebbe 230, mentre in uno spazio a 4 dimensioni, di cui noi comuni mortali non conosciamo se esiste (vedi cosa ne pensava Gino Loria nel 1907), vi sarebbero 4783 sottogruppi di simmetria.
Per una introduzione che stimoli alcune considerazioni sulla simmetria con riferimenti scientifici ma anche divertenti vedi questo post.
Di seguito si riportano esempi schematici dei 26 sottogruppi di cui sopra.
Le figure sono state tratte dal libro di Lionel Mach e Philip Steadman, La geometria dell'ambiente, Ed. Mazzotta, Padova, 1974, pp. XXXIII + 361, (ed. originale: The Geometry of Environment, 1971).
Analoghe figure ed esempi si trovano anche nei più recenti e reperibili libri: Maria Dedò, Forme, Simmetria e topologia, Ed. Zanichelli, Padova 1999, pp. V + 408; AA.VV., Simmetria: una scoperta matematica, Ed. Polipress, Milano 2007, pp. XII + 80.



+Prospettografo.jpg)
+Disegno+preparatorio.jpg)












